In our daily lives? Well, maybe not that much. But let me tell you, even a primary school student actually uses integrals (or at least, simple formulas derived from integrals) without actually knowing it. Before starting the explanation, I want to show you the simple expression for a definite integral just to get a bit familiar with it:

If you don't know the purpose of that apostrophe, I strongly recommend you to read this thread first.
Now, let's begin.
Think of a rectangle with length of 6 cm and width of 4 cm. Can you calculate the area of that rectangle? Easy, right? You actually implicitly used a double integral while calculating, but that integral is so easy that no one actually uses it in integrals and instead memorizes outcomes of each of those integrals, which are in fact the lengths of the sides.
First, let's take a look at our little rectangle:
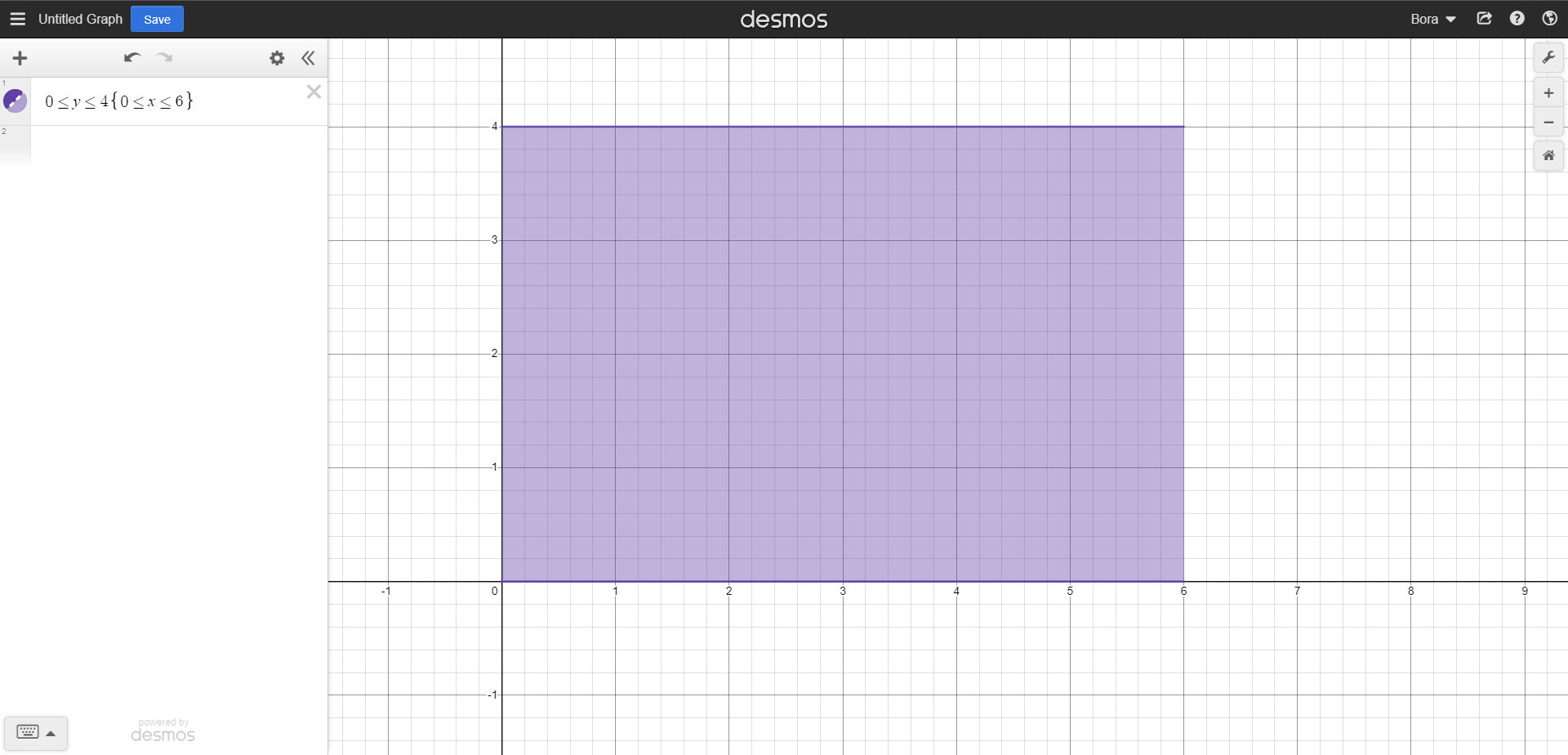
Let's say long side of our rectangle starts at the point (0, 0) and ends at the point (6, 0). So, for the long side, x goes from 0 to 6. Now we must think that we split that long side into some equal pieces. There are a lot of ways to do that. We can split it into 6 pieces of 1 cm parts, 12 pieces of 0.5 cm parts... Where does it end? Well, at the point where we have infinite amount of parts. To do that, we must think that line contains infinite amount of infinitely small pieces (dx).
Now, to find the length, we must sum all pieces. Since we have infinite amount of infinitely small pieces, we cannot calculate this summation as we do 2 + 2. We must think of a new concept. That's where the integrals shine.
Check out the first image of this thread again. Since x goes from 0 to 6, our lower limit (b) must be 0 and upper limit (a) must be 6. We don't have a function here, just the length. So instead of f'(x), we have 1 there. Now, let's talk how we are going to compute that integral, starting with indefinite integrals.
The only difference between indefinite and definite integrals is that definite integrals have limit values. While solving integrals, we must first determine the variable for which we are going to solve it. That variable is given us by the expression end of it, dx. To solve the integral, we must increment all elements' exponents that contain x by 1, then divide those elements by their new exponents. In this case, our integral looks something like this since x^0 = 1:
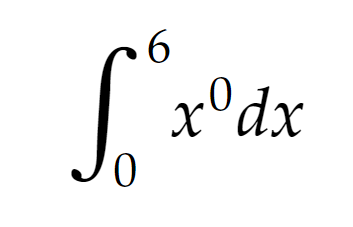
x^0 transforms to (x^1)/1, so, it's just plain and simple x. Since those limits were for x, we can say that this integral is equal to 6 - 0, so 6. Let's see how this integral looks on our rectangle:
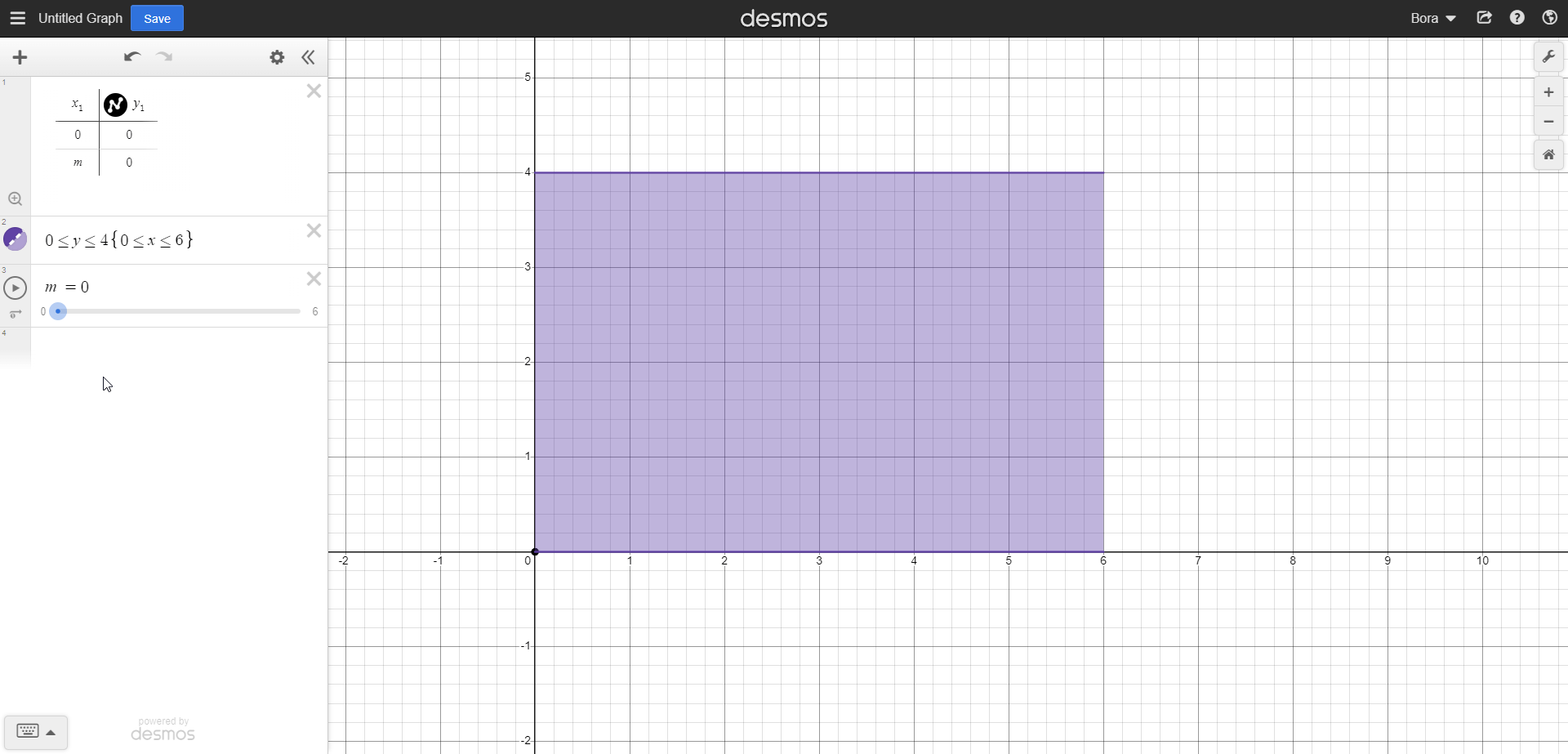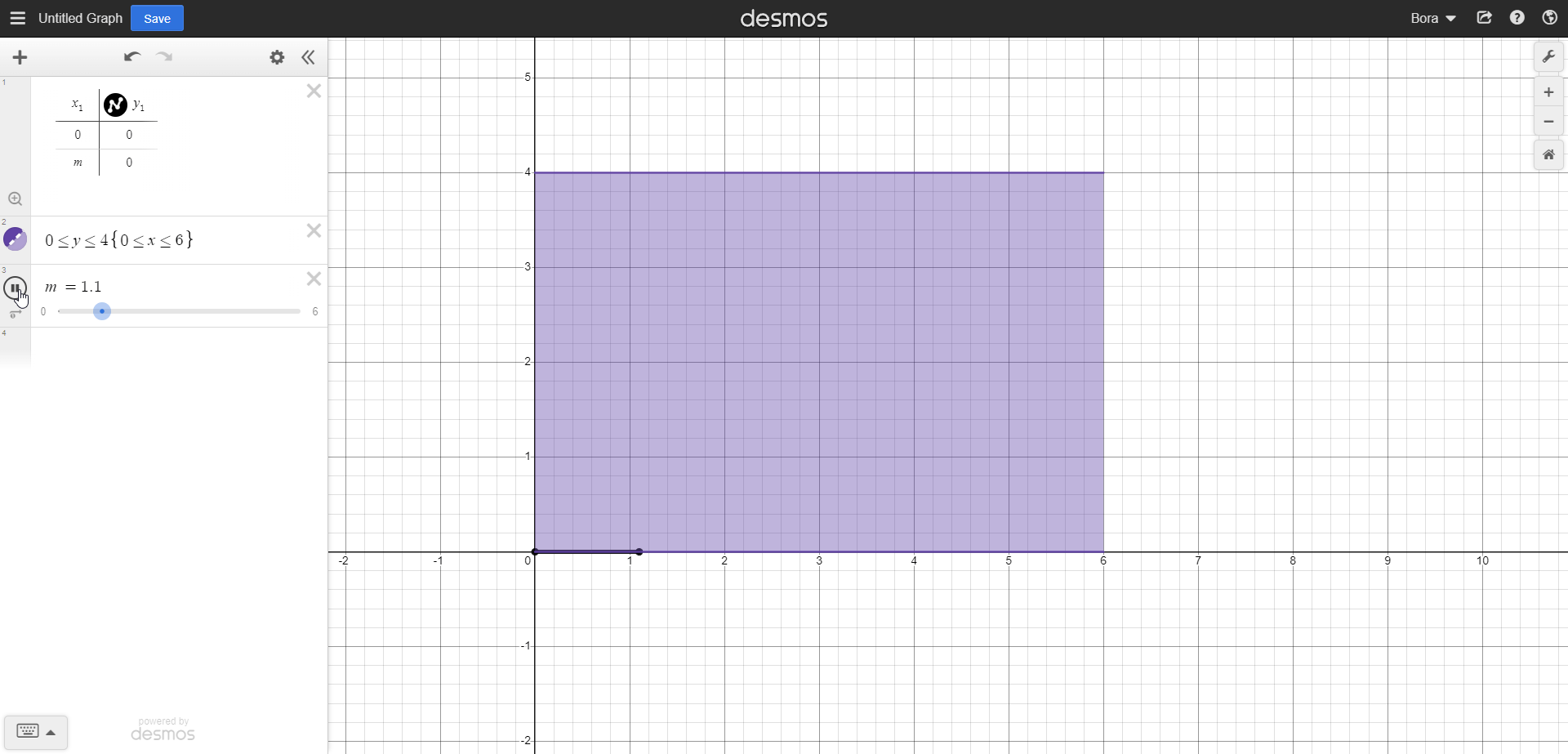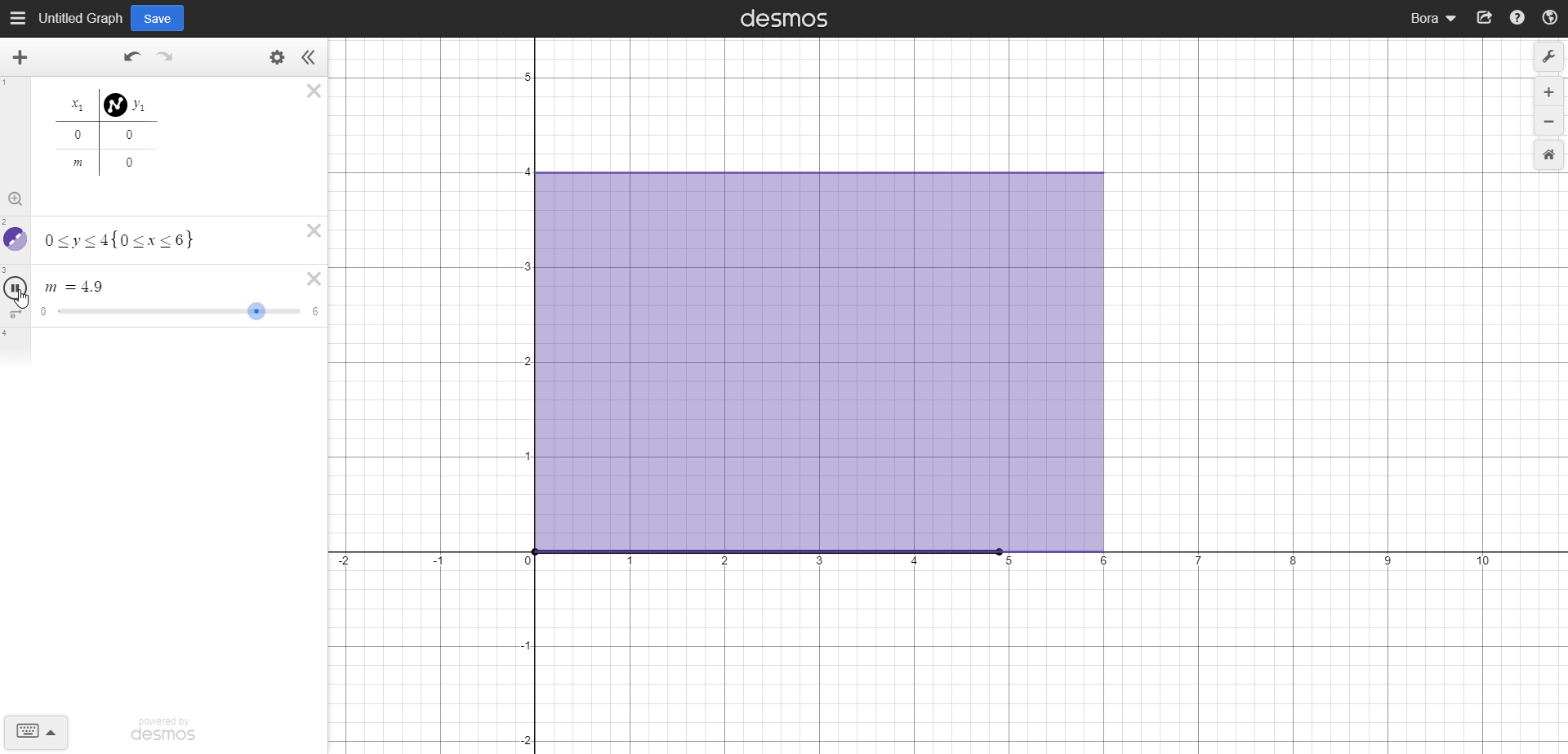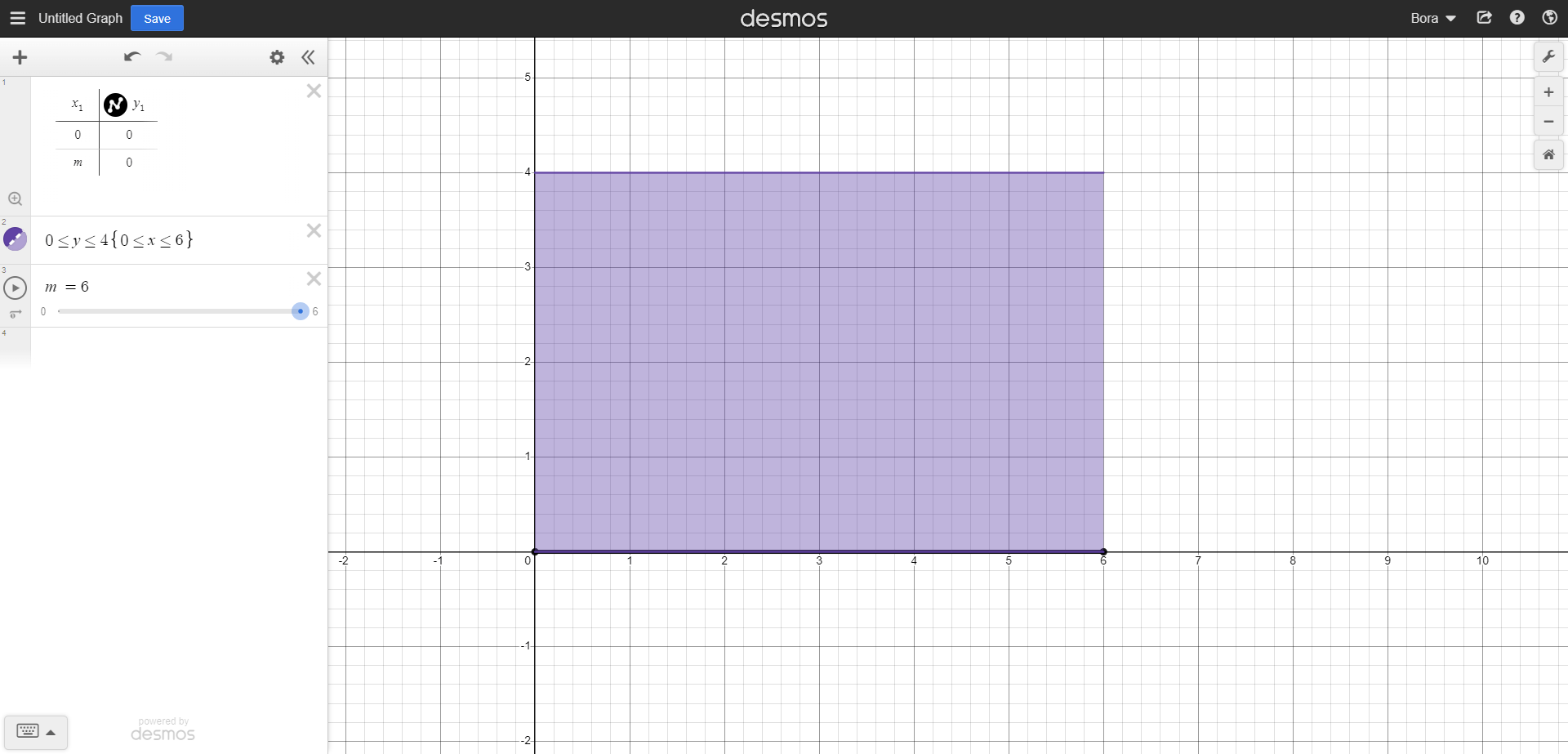
As shown in the GIF, we scanned the length of our rectangle with this integral. Now we should scan our rectangle upwards using the length element, so we can scan the full area. Now, our integrand should have 0 and 4 as lower and upper limits, respectively. So, it should look something like this:
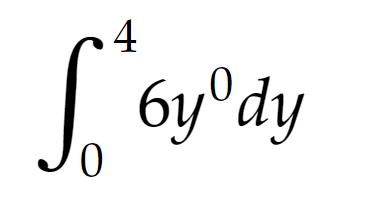
Notice that the differential element has changed, because our scanning direction has changed. Our integrand comes out as 6y and since limits are 0 and 4, the result would be 6x4 - 6x0 = 24. Indeed, we can validate that a rectangle with 4 cm and 6 cm of sides has an area of 24 cm^2. And this is what the last scanning would look like on our rectangle:
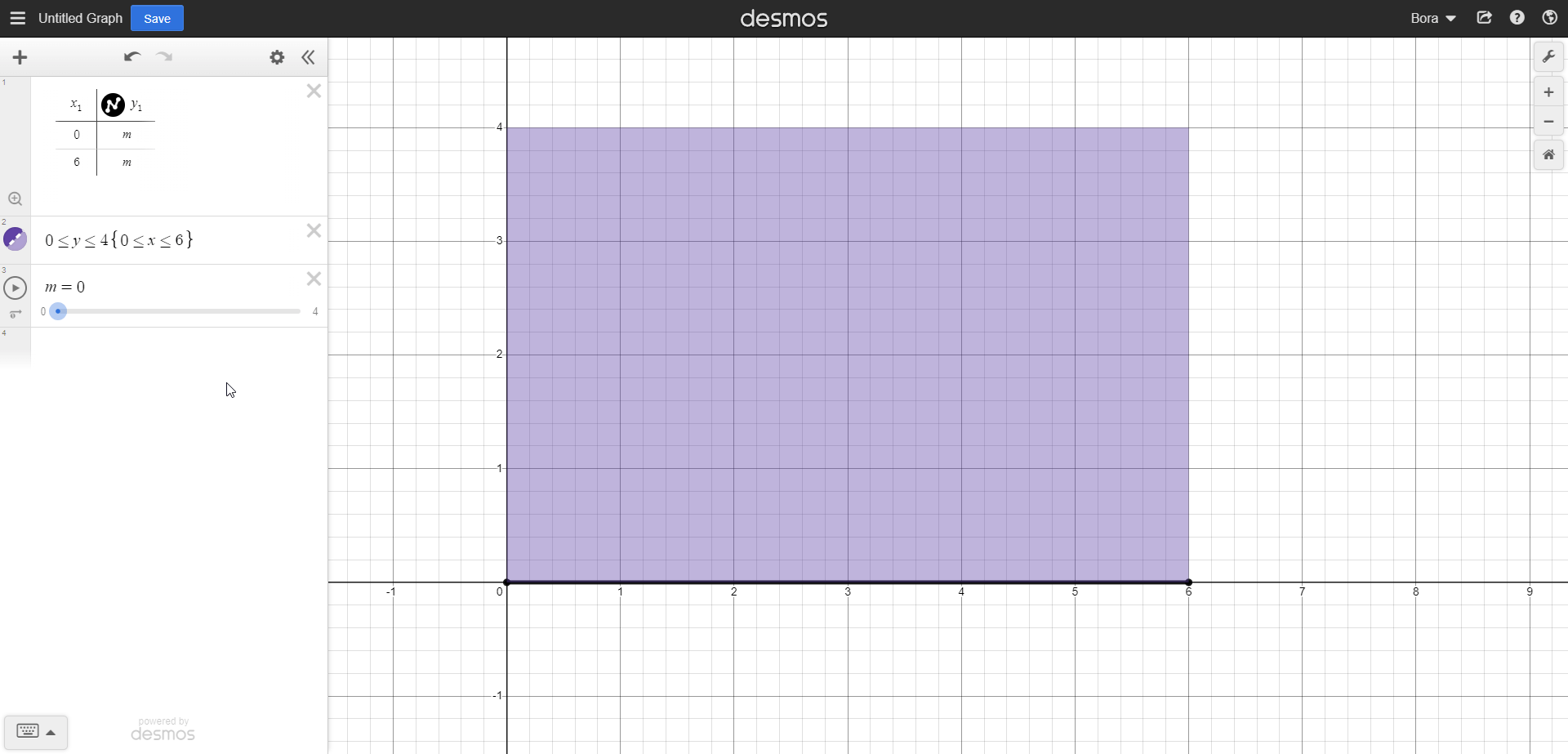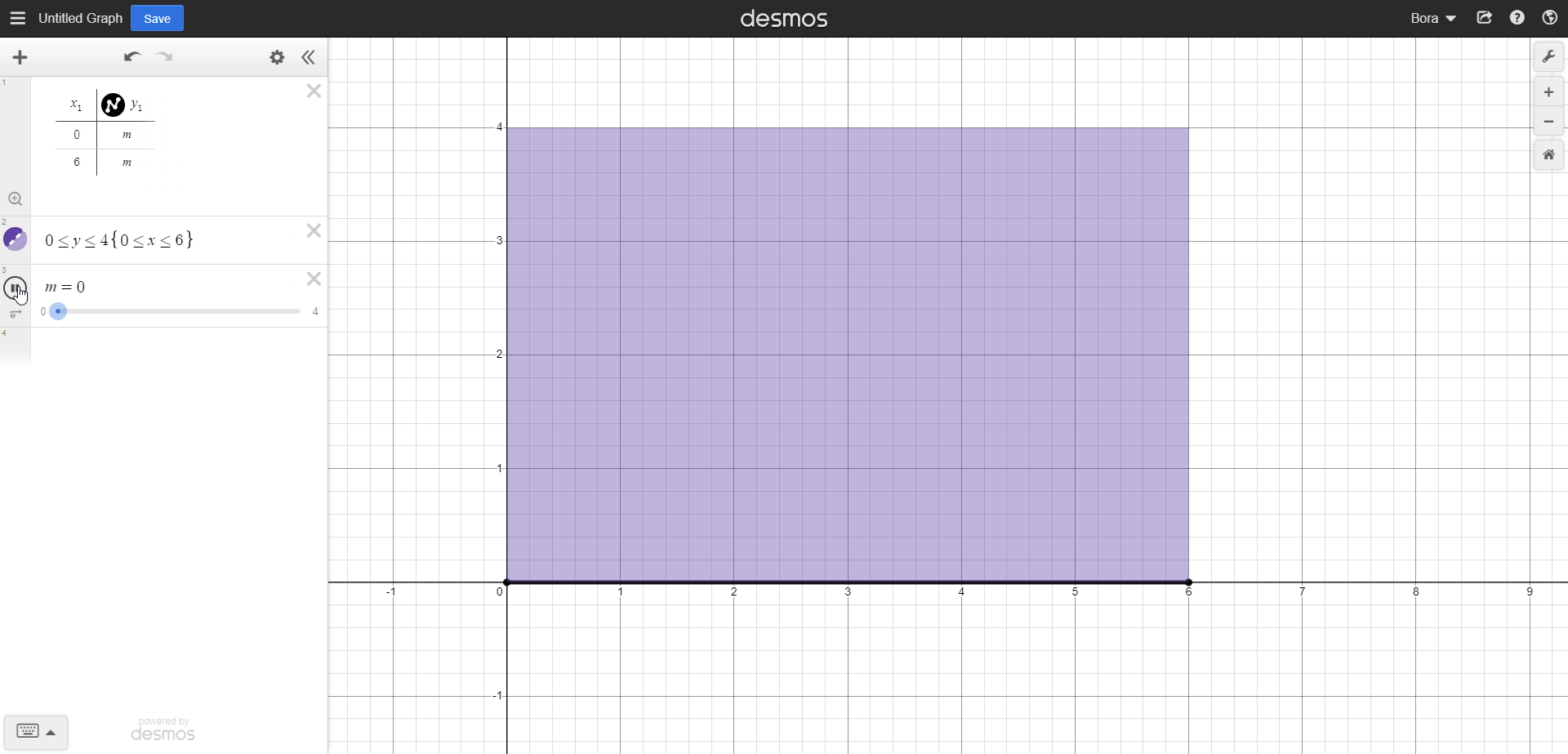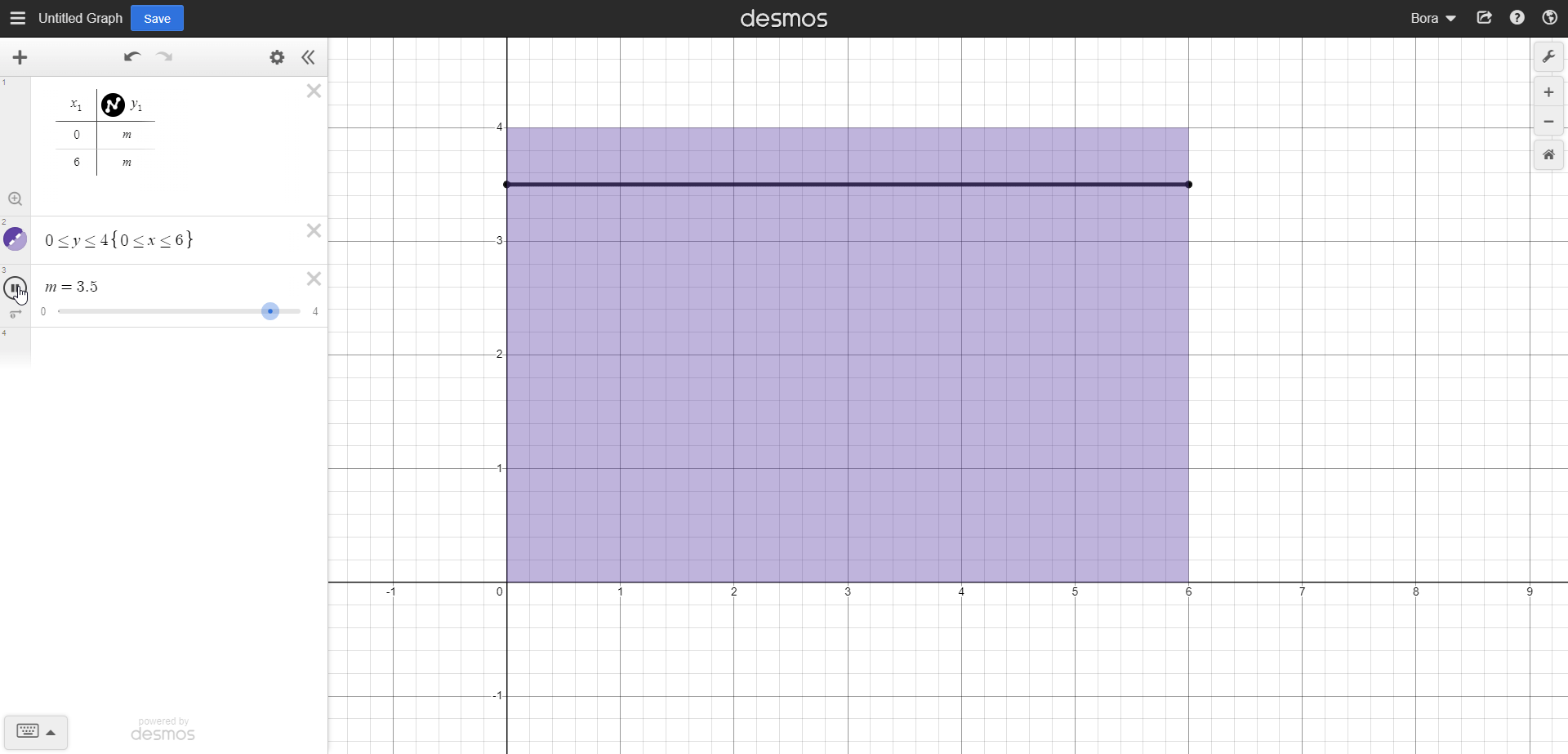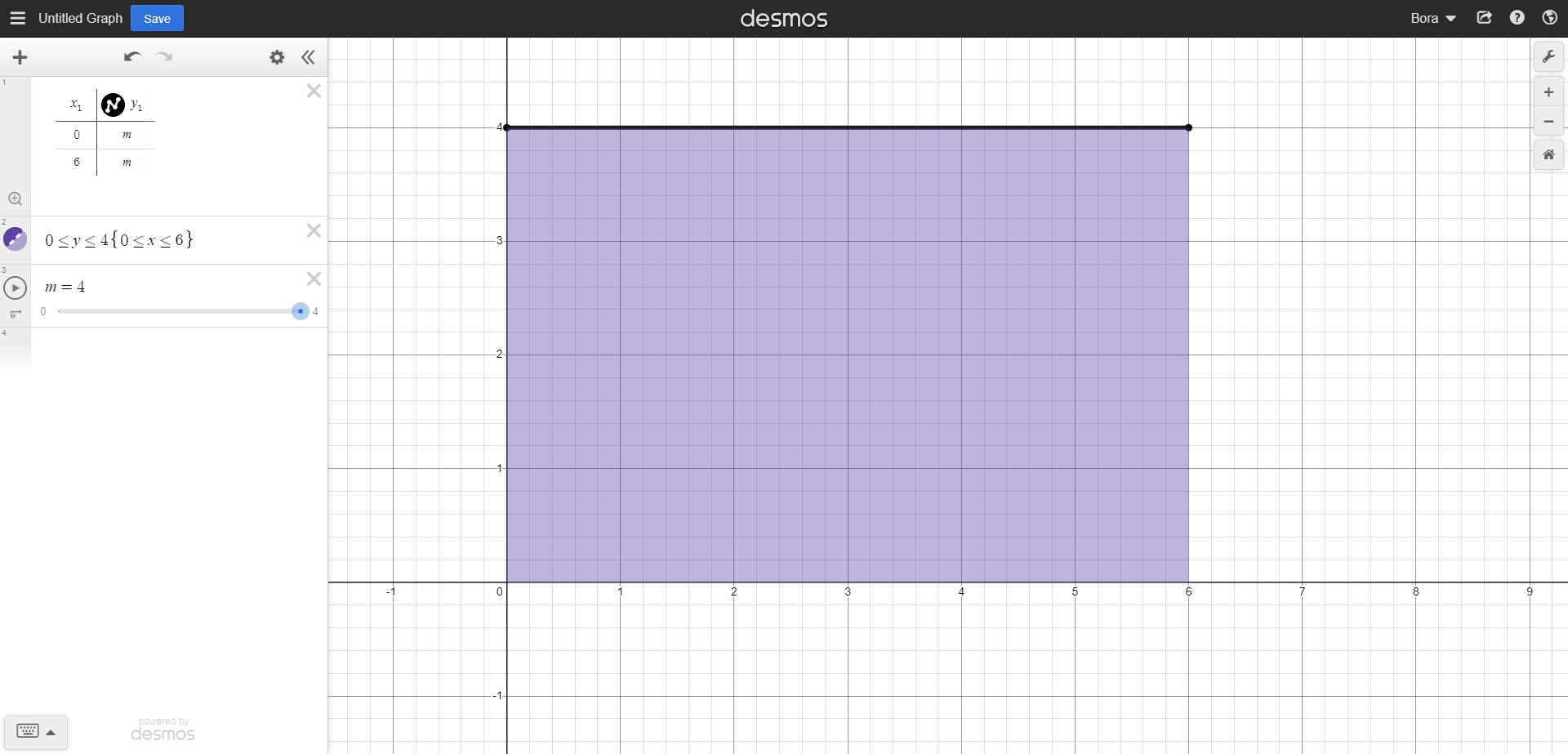
For this case, integration order wouldn't make a difference, we could have started scanning through +y axis then do the rest, it wouldn't change the result. But that wouldn't always be the same. This is what our integrals combined looks like:
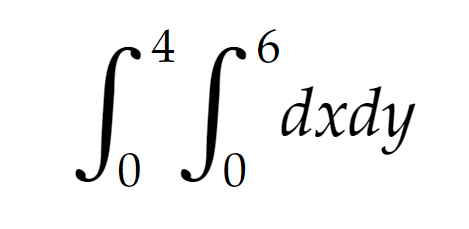
Now, let's think of a silly shape. Let's say, area lies below the f(x) = (x^2)/6 where 0 < x < 7. This is what our function looks like:

How are we going to calculate that area? It doesn't look anything like our good old rectangle. Well, Bernhard Riemann had an idea. We are going to split one axis (x-axis, in our example) into equal pieces, then mark their points on the function and create some columns. For example, if we split that length into 7 1 cm pieces and create columns, it would look something like this:
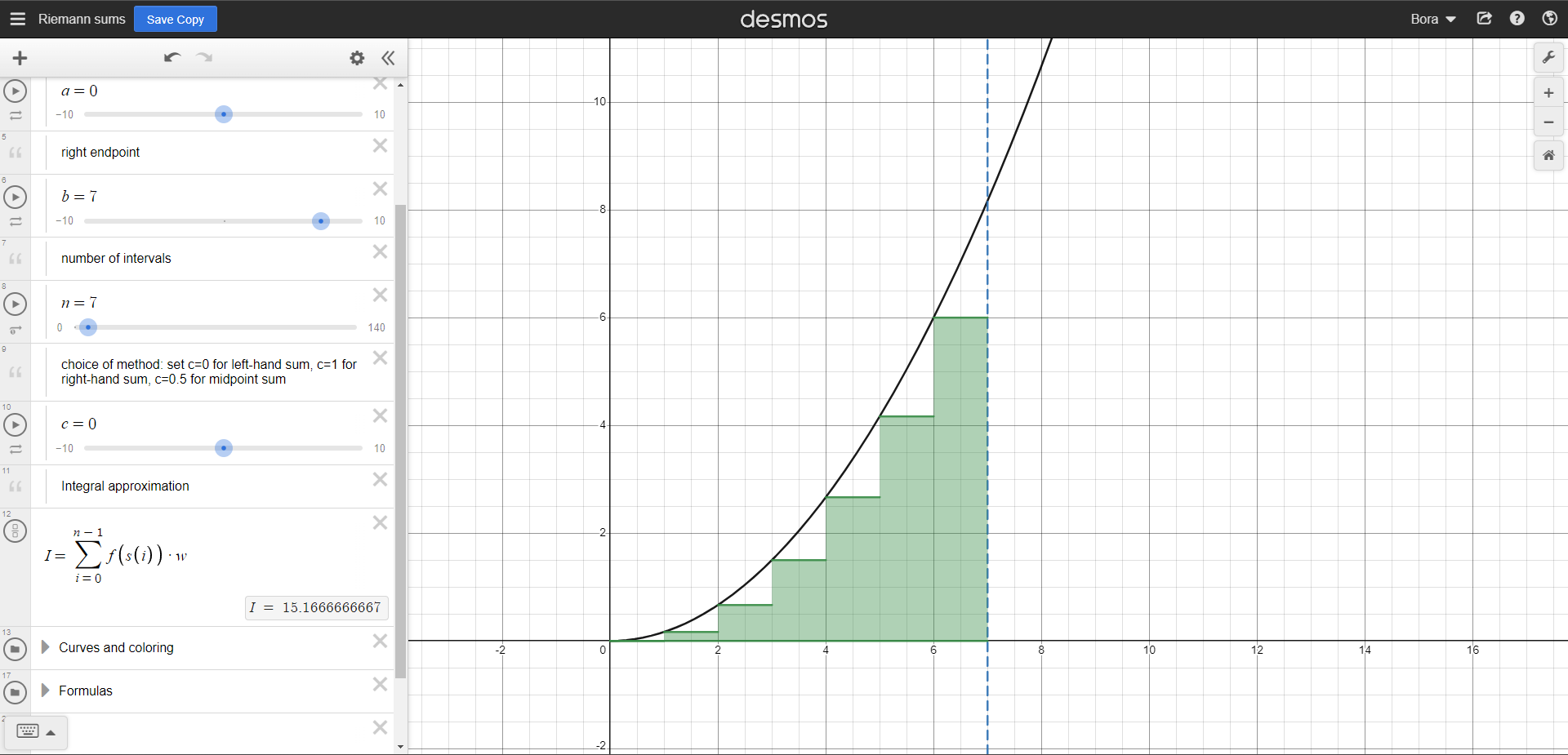
They sure have an area but we are still missing some places at the upper parts. Should we split it into even more pieces? Let's try 28 pieces:
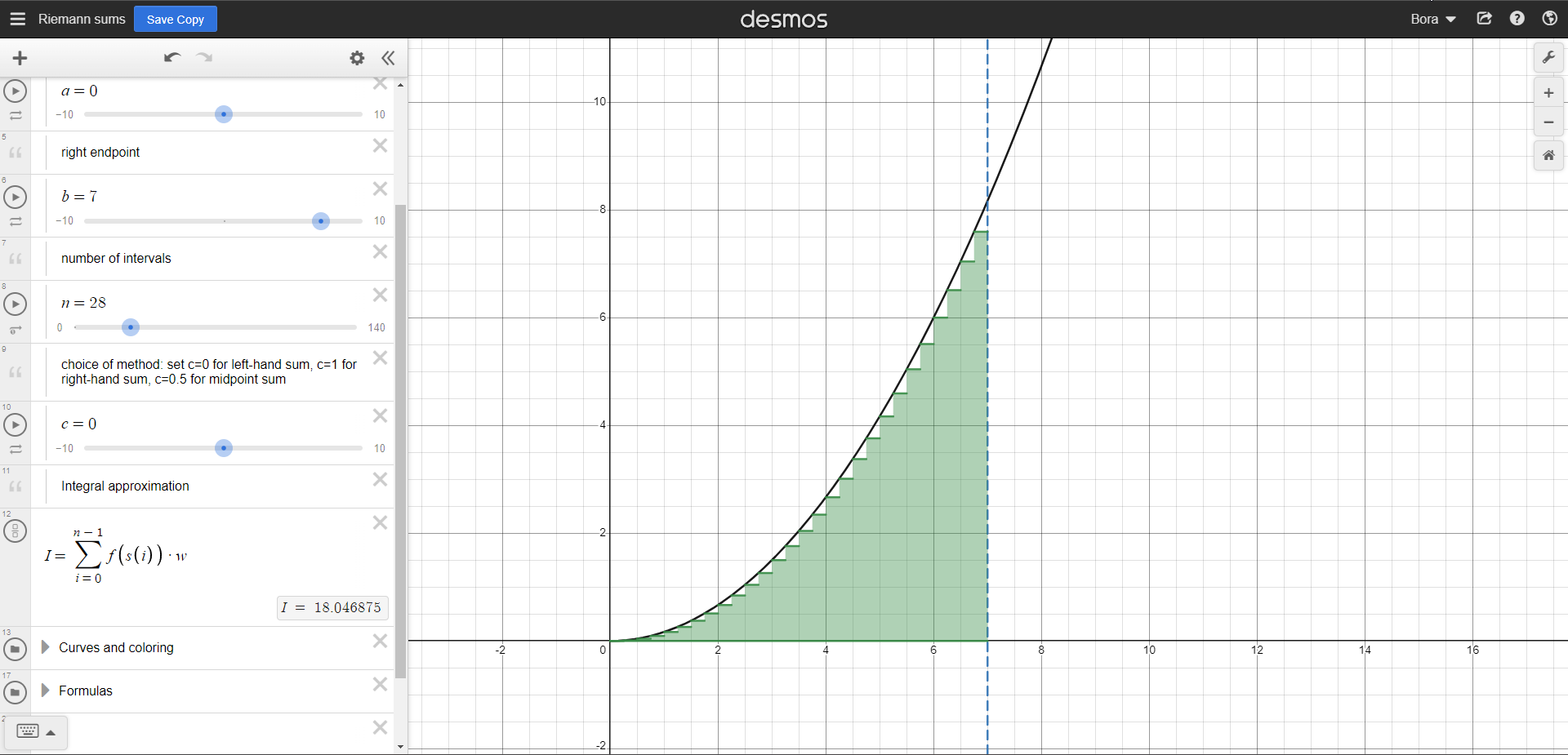
Better, but still not good enough. At that point, we must think that splitting it into infinitely many and infinitely small pieces.

That integral would look something like this:
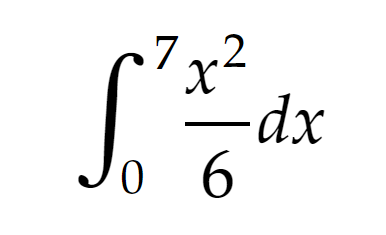
Solving the integral, we will get (x^3)/18 where x goes from 0 to 7. The result is 19,055... and it's disgusting, yes. But our shape is not a good looking one, so, all is well.
If you want to play with Riemann sums calculator, here is the link:

 www.desmos.com
www.desmos.com
If you don't know the purpose of that apostrophe, I strongly recommend you to read this thread first.
Now, let's begin.
Think of a rectangle with length of 6 cm and width of 4 cm. Can you calculate the area of that rectangle? Easy, right? You actually implicitly used a double integral while calculating, but that integral is so easy that no one actually uses it in integrals and instead memorizes outcomes of each of those integrals, which are in fact the lengths of the sides.
First, let's take a look at our little rectangle:
Let's say long side of our rectangle starts at the point (0, 0) and ends at the point (6, 0). So, for the long side, x goes from 0 to 6. Now we must think that we split that long side into some equal pieces. There are a lot of ways to do that. We can split it into 6 pieces of 1 cm parts, 12 pieces of 0.5 cm parts... Where does it end? Well, at the point where we have infinite amount of parts. To do that, we must think that line contains infinite amount of infinitely small pieces (dx).
Now, to find the length, we must sum all pieces. Since we have infinite amount of infinitely small pieces, we cannot calculate this summation as we do 2 + 2. We must think of a new concept. That's where the integrals shine.
Check out the first image of this thread again. Since x goes from 0 to 6, our lower limit (b) must be 0 and upper limit (a) must be 6. We don't have a function here, just the length. So instead of f'(x), we have 1 there. Now, let's talk how we are going to compute that integral, starting with indefinite integrals.
The only difference between indefinite and definite integrals is that definite integrals have limit values. While solving integrals, we must first determine the variable for which we are going to solve it. That variable is given us by the expression end of it, dx. To solve the integral, we must increment all elements' exponents that contain x by 1, then divide those elements by their new exponents. In this case, our integral looks something like this since x^0 = 1:
x^0 transforms to (x^1)/1, so, it's just plain and simple x. Since those limits were for x, we can say that this integral is equal to 6 - 0, so 6. Let's see how this integral looks on our rectangle:
As shown in the GIF, we scanned the length of our rectangle with this integral. Now we should scan our rectangle upwards using the length element, so we can scan the full area. Now, our integrand should have 0 and 4 as lower and upper limits, respectively. So, it should look something like this:
Notice that the differential element has changed, because our scanning direction has changed. Our integrand comes out as 6y and since limits are 0 and 4, the result would be 6x4 - 6x0 = 24. Indeed, we can validate that a rectangle with 4 cm and 6 cm of sides has an area of 24 cm^2. And this is what the last scanning would look like on our rectangle:
For this case, integration order wouldn't make a difference, we could have started scanning through +y axis then do the rest, it wouldn't change the result. But that wouldn't always be the same. This is what our integrals combined looks like:
Now, let's think of a silly shape. Let's say, area lies below the f(x) = (x^2)/6 where 0 < x < 7. This is what our function looks like:
How are we going to calculate that area? It doesn't look anything like our good old rectangle. Well, Bernhard Riemann had an idea. We are going to split one axis (x-axis, in our example) into equal pieces, then mark their points on the function and create some columns. For example, if we split that length into 7 1 cm pieces and create columns, it would look something like this:
They sure have an area but we are still missing some places at the upper parts. Should we split it into even more pieces? Let's try 28 pieces:
Better, but still not good enough. At that point, we must think that splitting it into infinitely many and infinitely small pieces.
That integral would look something like this:
Solving the integral, we will get (x^3)/18 where x goes from 0 to 7. The result is 19,055... and it's disgusting, yes. But our shape is not a good looking one, so, all is well.
If you want to play with Riemann sums calculator, here is the link:
